Toute étude statistique a pour but d'obtenir des informations sur un caractère observé sur une population ( véhicules, élèves ... ) tels que la fréquence, l'effectif cumulée, la moyenne, les quartiles. Une étude statistique utilise régulièrement des diagramme ou des histogrammes. IL existe 2 sortes de caractères, les qualitatif que l'on ne peut pas mesurer et les quantitatifs qu'on peut mesurer.
I) La fréquence :
La fréquence est la population ayant une classe du caractère observé sur la population totale observée. Ainsi, si sur 10 personnes ( population totale ) seul 2 ont 10 ans, la fréquence de la classe du caractère age : " 10 ans " est de 2/10 soit 0.2. Les autres individus de la population ont une classe du caractère différent : 6 ont 12 ans, 1 a 14 ans et 1 a 16 ans. Pour chaque caractère il y a une fréquence. La fréquence du caractère 12 ans est 6/10 = 0.6... Dans une étude statistique, le total des fréquences est égal à 1.
La fréquence cumulée d'1 classe est l'addition des fréquences de toutes les classes du caractères jusqu'à ce dernier. Ainsi, la fréquence cumulée de 14 ans pour l’exemple précédent est : 0.2 ( 10 ans ) + 0.6( 12 ans ) + 0.1 ( 14 ans ) = 0.9
II) Médiane, quartiles et moyenne :
La médiane et les quartiles sont des divisions au sein d'un caractère.
La médiane est le nombre limite à partir duquel 50% des valeurs de la série lui sont inférieurs et 50% lui sont supérieurs.
Le premier quartile est le nombre pour limite pour lequel 25% des valeurs de la série lui sont inférieurs et 75% lui sont supérieurs.
Le 3e quartile est le nombre limite pour lequel 75% des valeurs de la série lui sont inférieurs et 25% lui sont supérieurs.
Remarque : la médiane est donc le second quartile.
La moyenne d'1 série statistique se calcule à l'aide des effectifs des classes de cratère ( pour notre exemple, 2 personnes ont 10 ans, 6 ont 12 ans, 1 a 14 ans et 1 a 16 ans); mais aussi grâce à la classe elle même ( 10 ans / 12 ans / 14 ans / 16 ans ), ou à un centre de classe si les classes correspondent à un intervalle ( par exemple, de 10 à 12 ans, le centre de classe est 11 ans ). Pour calculer une moyenne, on utilise une fraction de ce type :
effectif de la classe 1 * classe 1 + effectif de la classe 2 * classe 2 ... ( et ça continue selon le nombre de classe que l'on a)
---------------------------------------------------------------------------------------------------------
effectif total de la série statistique
Dans notre exemple, ça donnerait cela :
2*10 + 6* 12 + 1*14 +1*16
-------------------------------------- = 12.2 La moyenne de cette série statistique est 12.2.
10
Ont ne peux calculer les médianes, quartiles moyennes qu'avec un caractère quantitatif.
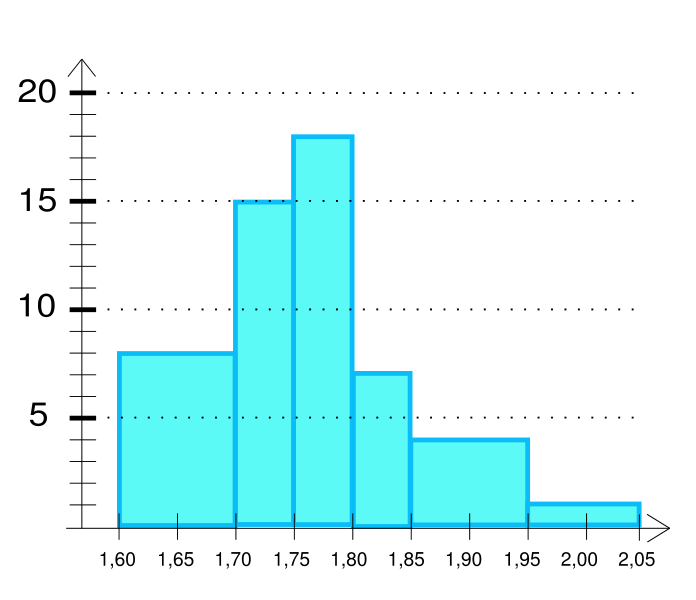
III) Histogramme :
Un histogramme est une figure représentant les différentes classes d'une série statistique ( caractère quantitatif ) sous formes de rectangle dont l'aire est proportionnelle à l'effectif. La figure se fait sur un repère. Afin de construire un histogramme, il nous faut : l'amplitude classe, l'effectif des classes, et le coefficient de classe.
1) la largeur du rectangle :
la largeur du rectangle correspond à l'amplitude de classe : c'est à dire, lorsque notre valeur de classe est un intervalle ( de 10 à 20 par exemple), la soustraction du nombre le plus haut par le plus bas de l'intervalle. ( 20-10 = 10, l'amplitude de classe est 10). La largeur du rectangle = l'amplitude de classe.
2) La hauteur du rectangle :
Pour connaître la hauteur du rectangle, il nous faut connaître le coefficient de classe. Pour cela, on observe toutes les classes de la série et on repère laquelle a la plus petite amplitude de classe. Son coefficient sera 1. Ensuite, on observe les autres amplitudes de classes et on voit à combien de fois elles sont égales à l'amplitude de classe la plus petite ( si 10 est l'amplitude de classe la + petite, 20 est égale à 2 fois 10 ). Leur coefficient de classe est autant de fois plus grand ( 20 = 2*10, le coefficient de la classe qui a pour amplitude 20 est 2).
Maintenant que nous avons le coefficient de classe, il suffit de diviser l'effectif de chaque classe par son coefficient et on trouve la hauteur du rectangle de chaque classe.
exemple d'histogramme :
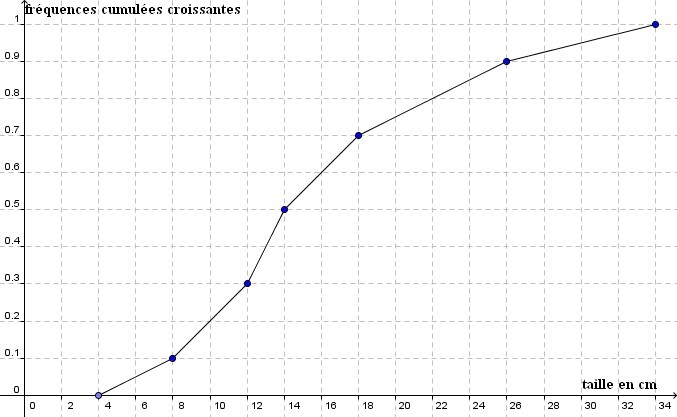
IV) Polygone des fréquences :
Un polygone des fréquences est une autre représentation d'une série statistique dans un repère : il nous faut là aussi des classes étant des intervalles ainsi que les fréquences cumulées des classes.
Il s'agit juste de trouver les points de coordonnées d'un point pour chaque classe.
Chaque point correspond à 1 classe. Son abscisse est le nombre clôturant l'intervalle ( de 10 à 20, 20 est le nombre clôturant l'intervalle ) et son ordonnée est la fréquence cumulée de la classe Lorsuq'on a placé tous les points de la série statistique, on les relie. Si le trait reliant tous les points ne fait que monter, on a obtenu notre polygone.
exemple de polygone :
Aucun commentaire:
Enregistrer un commentaire